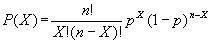EJERCICIOS PÁG.113

DISTRIBUCIÓN BINOMIAL E HIPERGEOMÉTRICA

Distribución de Probabilidad Distribución de Probabilidad Binomial

Un experimento de Bernoulli puede resultar en un éxito con una probabilidad p y en un fracaso con una probabilidad de q = 1−p Entonces la distribución de probabilidad de la variable aleatoria binomial X, el número de éxitos en n experimentos independientes, es: 

b(x; n, p) = px qn−x x = 0, 1, 2, 3,.........., n. 

La distribución binomial aparece cuando estamos interesados en el número de veces que un suceso A ocurre (éxitos) en n intentos independientes de un experimento. 

P. ej.: # de caras en n lanzamientos de una moneda.

Si A tiene probabilidad p (probabilidad de éxito) en un intento, entonces 1-p es la probabilidad de que A no ocurra (probabilidad de fracaso).

MODELO MATEMÁTICO:

Donde:

P(X) = probabilidad de X éxitos dados los parámetros n y p

n = tamaño de la muestra

p = probabilidad de éxito

1 – p = probabilidad de fracaso

X = número de éxitos en la muestra ( X = 0, 1, 2, …….. n)

Distribución de Probabilidad Distribución de Probabilidad Hipergeométrica

La distribución de probabilidad de la variable aleatoria hipergeométrica X, el número de éxitos en una muestra de tamaño n seleccionada de N posibles resultados, de los cuales k son considerados como éxitos y N − k como fracasos.

EVIDENCIA:

VARIABLES ALEATORIAS: DISCRTETAS Y CONTINUAS

DISTRIBUCIÓN DE LA PROBABILIDAD DISCRETA

VARIABLE ALEATORIA DISCRETA

Para la descripción de una variable aleatoria discreta, se especifican los posibles valores de la variable con sus respectivas probabilidades. Sea X una variable aleatoria que toma valores x1, x2, . . . , xn, . . ..

 Entenderemos por P(X = xi) como la probabilidad del suceso

 X −1 (xi) = {w ∈ Ω : X(w) = xi} = A ∈ Q.

DISTRIBUCIÓN DE LA PROBABILIDAD DISCRETA

Una distribución discreta describe la probabilidad de ocurrencia de cada valor de una variable aleatoria discreta. Una variable aleatoria discreta es una variable aleatoria que tiene valores contables, tales como una lista de enteros no negativos.

Con una distribución de probabilidad discreta, cada valor posible de la variable aleatoria discreta puede estar asociado con una probabilidad distinta de cero. Por lo tanto, una distribución de probabilidad discreta suele representarse en forma tabular.

VARIABLE ALEATORIA CONTINUA

Las variables aleatorias continuas se describen por medio de una función real de variable real, a la que se denomina función de densidad, que surge como la generalización de las curvas de frecuencias asociadas a los histogramas, cuando la amplitud de los intervalos se considera infinitamente pequeña. Llamaremos función de densidad de una variable aleatoria X a una función real f(x) no negativa    (f(x) ≥ 0) tal que

 Z +∞ −∞ f(x) dx = 1

y de forma que es posible calcular la probabilidad de que X tome valores en un cierto intervalo [a, b], por integración 

P(a < X < b) = Z b a f(x) dx. 

DISTRIBUCIÓN DE LA PROBABILIDAD CONTINUA

Una distribución continua describe las probabilidades de los posibles valores de una variable aleatoria continua. Una variable aleatoria continua es una variable aleatoria con un conjunto de valores posibles (conocido como el rango) que es infinito y no se puede contar.

Las probabilidades de las variables aleatorias continuas (X) se definen como el área por debajo de la curva. Por lo tanto, solo los rangos de valores pueden tener una probabilidad diferente de cero. La probabilidad de que una variable aleatoria continua equivalga a algún valor siempre es cero.

EVIDENCIA:

FORMAS DE REPRESENTACIÓN GRÁFICA

Variables discretas

Gráficos para variables discretas Cuando representamos una variable discreta, usamos el diagrama de barras cuando pretendemos hacer una gráfica diferencial. Las barras deben ser estrechas para representar que los valores que toma la variable son discretos. El diagrama integral o acumulado tiene, por la naturaleza de la variable, forma de escalera.

Variables continuas

Cuando las variables son continuas, utilizamos como diagramas diferenciales los histogramas y los polígonos de frecuencias.

Un histograma se construye a partir de la tabla estadística, representando sobre cada intervalo, un rectángulo que tiene a este segmento como base. El criterio para calcular la altura de cada rectángulo es el de mantener la proporcionalidad entre las frecuencias absolutas (o relativas) de cada intervalo y el área de los mismos. 

El polígono de frecuencias se construye fácilmente si tenemos representado previamente el histograma, ya que consiste en unir mediante líneas rectas los puntos del histograma que corresponden a las marcas de clase. 

EVIDENCIA:

ESPERANZA MATEMÁTICA

ESPERANZA MATEMÁTICA

La esperanza matemática o valor esperado de una variable aleatoria discreta es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso.

Esta hace referencia a la ganancia promedio, teniendo su origen en los juegos de azar, esperando esta, la ganancia promedio cuando un jugador hace un gran número de apuestas.

Si la esperanza matemática es cero e(x)=0, entonces quiere decir que el juego es equitativo, no hay ventaja ni para el jugador, ni para la banca.

Para una variable aleatoria discreta con valores posibles  y sus probabilidades representadas por la función de probabilidad  la esperanza se calcula como ejemplo:

Para una variable aleatoria absolutamente continua, la esperanza se calcula mediante la integral de todos los valores y la función de densidad :

La definición general de esperanza se basa, como toda la teoría de la probabilidad, en el marco de la teoría de la medida y se define como la siguiente integral:

EVIDENCIA: