Distribución de Probabilidad Distribución de Probabilidad
Binomial
Un experimento de Bernoulli puede resultar en un éxito con una
probabilidad p y en un fracaso con una probabilidad de q = 1−p
Entonces la distribución de probabilidad de la variable aleatoria
binomial X, el número de éxitos en n experimentos
independientes, es:
b(x; n, p) = px qn−x x = 0, 1, 2, 3,.........., n.
La distribución binomial aparece cuando estamos
interesados en el
número
de veces que un suceso
A
ocurre (éxitos) en
n intentos independientes de un
experimento.
P. ej.: # de caras en n lanzamientos de una moneda.
Si
A tiene probabilidad
p (probabilidad de éxito) en un
intento, entonces 1-p es la probabilidad de que
A no
ocurra (probabilidad de fracaso).
MODELO MATEMÁTICO:
Donde:
P(X) = probabilidad de X éxitos dados los parámetros n y p
n = tamaño de la muestra
p = probabilidad de éxito
1 – p = probabilidad de fracaso
X = número de éxitos en la muestra ( X = 0, 1, 2, …….. n)
Distribución de Probabilidad Distribución de Probabilidad Hipergeométrica
La distribución de probabilidad de la variable aleatoria
hipergeométrica
X, el número de éxitos en una muestra de
tamaño
n seleccionada de
N posibles resultados, de los
cuales
k son considerados como éxitos y N
−
k como fracasos.

EVIDENCIA:
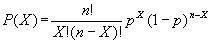


No hay comentarios.:
Publicar un comentario